I took a brief break from working on side projects to participate in the MCM (Mathematical Contest in Modeling) competition. I decided to compete in this competition mainly after enjoying and seeing success in the previous semester’s GDMS data analytics competition (post linked here) in which my team received an honorable mention in the beginner’s division. Again, my team consisted of friends Kali Liang (CMDA major) and Eric Fu (BIT major). Looking back on both of these competitions, I would definitely say the diversity in majors really helped in our ability to come together and perform, mainly due to our differences in perspective when it came to looking at the problem as a whole. Similar to the previous competition, we were given a .csv file with about 600 categories involving energy consumption and production rates per year in Arizona, California, New Mexico, and Texas, and were asked to come up with energy profiles for each state and to predict energy consumption and production in 2025 and 2050, all in the context of using cleaner energy sources. For reference, we tackled problem C (all problems linked here).
We used a mixture of VBA (Excel), Python, and R to analyze the given data. My main job was to determine which subsets of data were interesting and useful and to plot them using Python/matplotlib.
Moving on to the actual data analysis, we started by creating energy profiles for each of the four given states. We split our profiles into 3 graphs we deemed relevant, including overall energy consumption, overall energy production, and energy usage by sector in each state. The main hurdle for this section was deciding how to cut down the data to where each graph wouldn’t be too cluttered but the data would still be accurate enough to use. For instance, for energy consumption alone, each state’s initial graph had over 20 sub-plots, making the graph hard to read at first glance. This was due to the inclusion of ultimately insignificant values (for instance wood and waste energy consumption). As a result, we cut these insignificant sub-sets, facilitating visual analysis on each graph. The downside to this was not having a fully accurate representation of total consumption and production in each state, but we decided the sacrifice was worth it for the visual clarity provided. 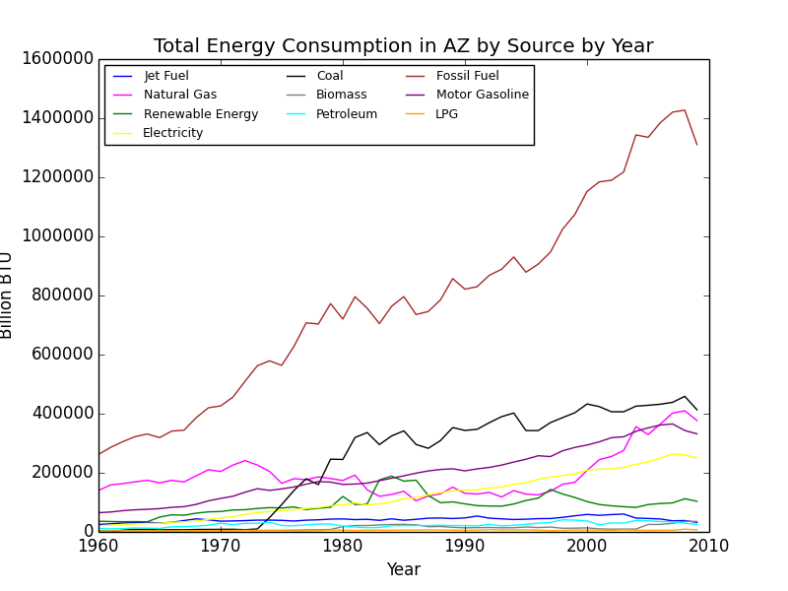
Energy consumption graph for Arizona. You can see that as the Y values approach 0, the higher the concentration of plot points (and this is after cutting more than 10 sub-sets).
Next, we moved onto attempting to define a more accurate illustration of the data set in regards to the context of the problem, renewable energy usage. We decided the best way to do this was to put everything in terms of the estimated amount of pollution each state was producing per year. We determined this value for each state per year by calculating the summation of each states energy consumption value multiplied by the transfer rate between that specific energy type and CO2 emissions. Essentially, we arranged Jet Fuel, Natural Gas, Coal, Petroleum, Motor Gasoline, and LPG consumptions per year in a single-column matrix and found its dot product with a constant single-column matrix that consisted of the conversion coefficients for that specific energy type and CO2 emissions, labeled C in the graphic below. We determined the conversion coefficients by pulling data from the EIA (here).

 Excerpt from our final paper detailing the values of the C conversion constant and giving Arizona’s numbers for 2009.
Excerpt from our final paper detailing the values of the C conversion constant and giving Arizona’s numbers for 2009.
Using the information above (Note: the structure of X_AZ follows that of C (in order of energy type from top to bottom, given in billion BTU. A conversion factor of 1000 Mill BTU / 1 Bill BTU was added) we are able to calculate an estimation of the CO2 emissions in Arizona in 2009 (X_AZ_2009 * C = 93307874.83 metric tons of CO2. Given the population of Arizona in 2009, we can then determine an estimation of CO2 emissions per capita of Arizona in 2009 (abt. 14 metric tons of C02 per capita). We then generalized this process in order to create a graph of CO2 emissions in each state per year.
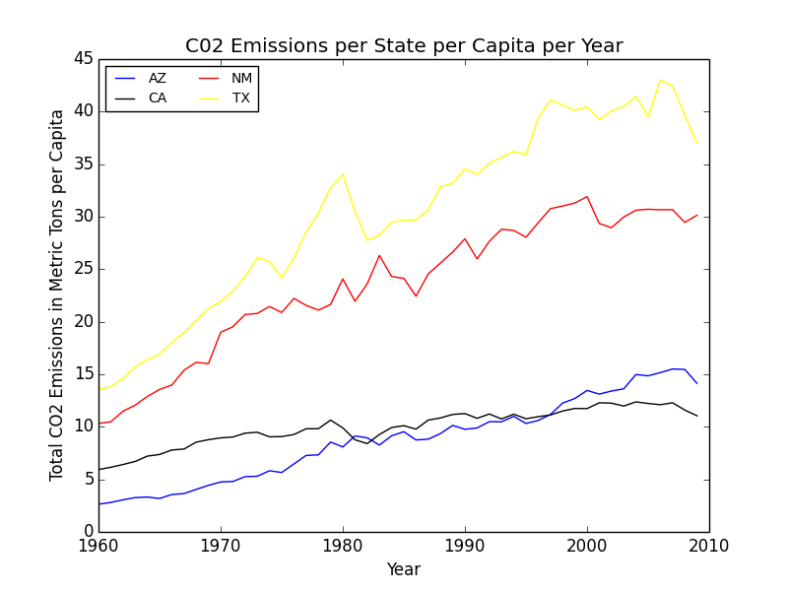
Graph detailing CO2 emissions per capita per year in each of the states. We used this information to generally rank each state in terms of pollution production, in order to circle back and create a discussion surrounding using cleaner energy sources.
Next came predicting energy consumption/production in 2025 in the context of cleaner energy usage. For this, as we began to run out of time (we only had four days for this competition) we resorted to using a basic linear regression to predict the values for 2025 and 2050. The main notable conclusion from this experiment was seeing how high energy consumption values were predicted to become, especially in regards to the very rapidly increasing CO2 emissions per capita for each state. As an example, total energy consumption in Arizona, using the linear regression model, was projected to increase by over 800,000 BTU. This, paired with the estimated increase in CO2 emissions per capita of abt. 5 metric tons per capita shows just how quickly pollution is projected to get out of control. Of the four states, Texas had the worst CO2 emission rates per capita estimated by 2050, seeing an increase of 37 metric tons per capita from 2009 (a projected value of abt 76 metric tons per capita). Again, we used these values to stress the importance of switching to more renewable energy sources in the coming years, before damage becomes irreversible.
Using all of the above data, we discussed in our conclusion the importance of moving away from commonly-used, bad for the environment energy sources. With the exponential increase in population in all of these states and really throughout the world, energy consumption and production has understandably seen a drastic increase in recent years. However, with the threat of global warming, each state needs to do whatever it can in order to slow or even reverse the effects brought on by these increased consumption and production rates.
I’m incredibly thankful to have competed in the GDMS competition prior to this competition, because without prior experience, we definitely would have had no idea where to start and probably would not have finished on time (of which we only barely did given the work detailed above, after making a numerous amount of assumptions ultimately weakening our argument). All in all, this competition was equally taxing on our mental health as it was fun to compete in. We look forward to participating in future data analysis competitions in the future. Unfortunately, we don’t hear back about the results until some time in April. If you want to see our final paper (written in LaTeX) in detail, you can find it here.