Towards the end of my first year at Virginia Tech, I oddly found myself with more free time than usual. Throughout the year I tried to focus on my neural network study when I could, but sadly, little time arose for me to pursue what I love. However, I always worked on small projects when I could. The majority of this time was spent geared towards learning Linux and Python, both of which I have become somewhat proficient in. Using these newfound skills, I looked back to my roots to see what improvements I could make on my original code from high school and to get back into the field of artificial intelligence in general. The main goal for this project was to create a short, dependable neural network algorithm for personal use in Python. I also wanted to create a system in which 2 neural networks were pitted against each other in some form of competition. I thought pong was a suitable game for this purpose because of its simplicity and competitive nature. My version of it stays, for the most part, true to the original game. 2 paddles, 1 ball, reset and score increase upon the ball exiting the left or right screen. After each bounce, the ball’s y velocity is randomly chosen between [2, 5] to add some randomness to where the ball will be when it reaches the left or right side of the screen. Pygame was used to render the components onto a window.
The general frame of mind I had while creating the neural network algorithm for this project was brevity and simplicity. One of the main issues with my Java implementation from a year ago was the fact that all of the weights were stored in a single 1D array, which isn’t ideal for many reasons. Mainly, it’s confusing to look at and understand the math behind extracting the correct weight at the correct time. To correct this, I switched it from a 1D array to a 3D array, in the format of [layer][input][output], layer being the current index in regards to the hidden layer, input being the “left” set, and output being the “right” set (i.e. input -> hidden, input is the “left” set and hidden is the “right” set). Although confusing at first due to my lack of experience with 3D arrays, I eventually came up with a good system that works just as fine as the original and is slightly easier to understand from an outsiders point of view. e

Example of a 3D weight storage system for a neural network with 2 input nodes, 1 hidden layer of 3 nodes, and 1 output node. The number of rows corresponds to the “input” layer (input -> hidden; input is the input layer, hidden -> output; hidden is the input layer) and the number of columns corresponds to the “output” layer (hidden and output in the above example).
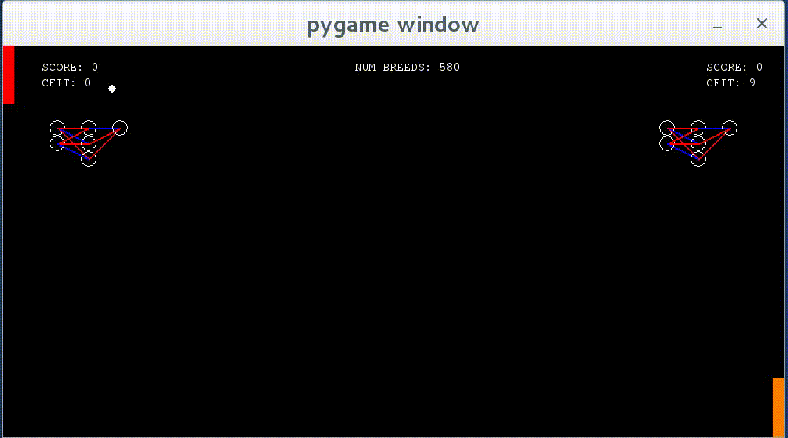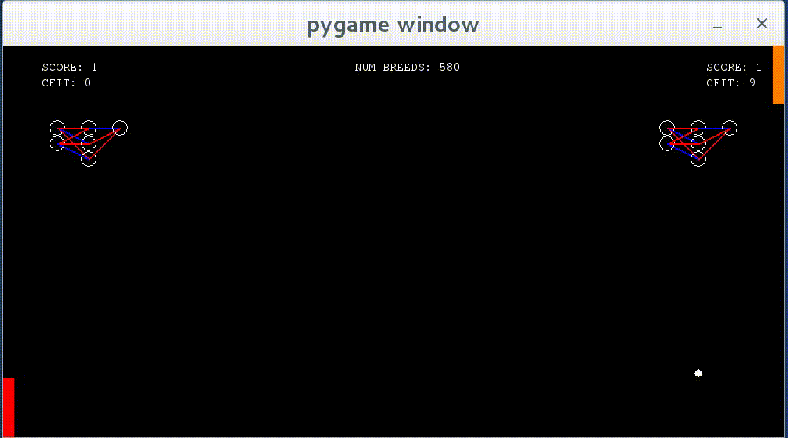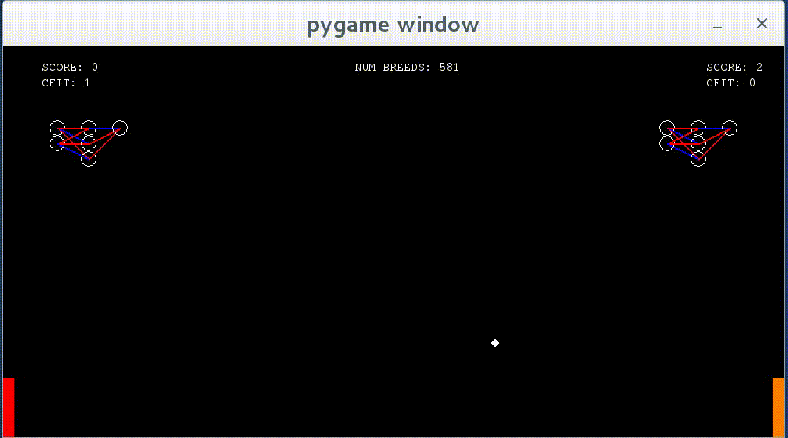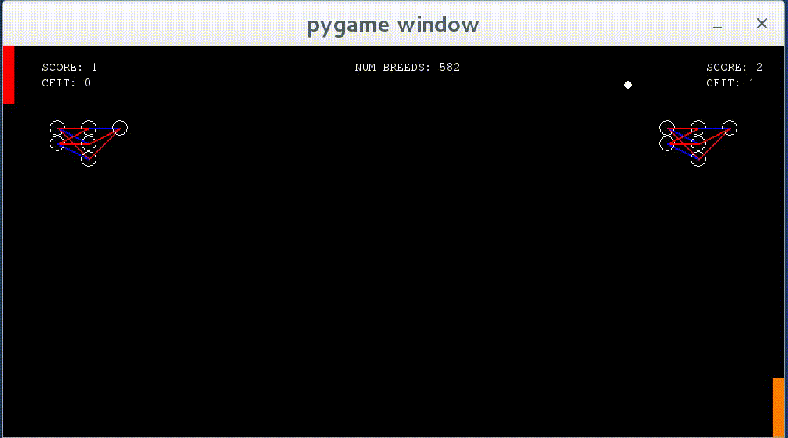
In this project, I experimented around with neural networks of varying sizes before settling on a simple 2 node input, 3 node hidden layer, and 1 node output network. The input was the vertical and horizontal distance between the paddle and the ball over the total height/width of the game window. When given more input nodes like the x and y velocity of the ball, it was observed that the neural networks were able to accurately predict where the ball would hit the paddle when it reached the side of the window (as opposed to just following the ball’s y component), but the time it took to reach this point was incredibly long and results varied over different situations (i.e. the angle the ball was approaching the paddle, etc.). Fitness was given based on how many matches the neural network won, but was punished twice as hard for every match (first to 3 points) lost (+1 for win, -2 for loss). A standard breeding process was performed after each match in which the parents were the 2 best performing networks in a population and the child was the worst, with the child weights having 2/3 chance of being from either of the parents and 1/3 chance of being the average of the parent weights. There was a 6% chance of any weight being erased and assigned a random value between (-1, 1). After each match, the loser was replaced by a randomly selected network from the population (it was ensured that the two networks playing each other were not the same one). Each paddle’s neural network can be seen displayed on its side of the board — each circle being a node and each line being a weight. A blue weight signifies a negative value and a red weight signifies a positive value.
Getting on to the actual project, the rate at which the neural networks became “good” at the game varied on each run. In my experience, it could be as short as 100 breeds, and as long as around 2000. However, for each run, the neural networks followed the same general pattern every time — make no attempt to move for the ball, show some attempt at chasing the ball or “reacting” the ball when it came close, and successfully chasing the ball.

Right when the program started. You can see the paddles move to either the top or the bottom of the screen, paying no attention to the ball.
Networks show some learning — they now react to the ball when it approaches them, though they do not move to the correct y value as of yet.

The end of the pattern. Networks demonstrate ability to chase after the ball and hit it every time. At this point, the match time is indefinite.
Although this project seemed simple at first, there were many different stages it went through while in development. At first, the input size for the neural networks was complex (including paddle location, ball location, ball velocity). However, after a lot of playing around, consistent improvement was shown when this list was refined to just the distance between the paddle and the ball. In retrospect, this makes sense, as decreasing the complexity of any problem makes it easier to solve. Although, maybe with more patience, a more unique strategy could have been developed with more inputs. I encourage you to download my source code and play around with yourself if you are at all interested in doing so (here).